Question

The graph of f(x)=2^x+1 passes through the points (-1 , 1) and (3 , 16).

Rebecca wants to find the average rate of change from x = -1 to x = 3. Here is her work:

3− ( −1) / 16−1 = 4/15
a. Explain Rebecca's error. (2 points)

b. Find the correct average rate of change. (2 points)

Answer 1

Please check the explanation.

Explanation:

Rebecca's ERROR

Rebecca wrongly used the formula to calculate the average rate of change from x = -1 to x = 3.

She should have used the correct formula to calculate the average rate of change from x = -1 to x = 3 which is:

Average rate = [f(3) - f(-1)] / [3 - (-1)]

But, she reversed the formula.

The correct solution

Considering the graph

`f\left(x\right)=2^x+1`

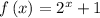
Rebecca wants to find the average rate of change from x = -1 to x = 3.

so

at x₁ = -1

`f\left(-1\right)\:=\:2^(-1)+1=(1)/(2)+1=(3)/(2)`

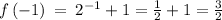
at x₂ = 3

`f\left(3\right)\:=\:2^3+1=8+1=9`

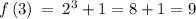
Using the formula, we can determine the average rate of change from x = -1 to x = 3

Average rate = [f(3) - f(-1)] / [ x₂ - x₁]

`=\:(\left[9\:-\:(3)/(2)\right])/(\left[3-\left(-1\right)\right])`

`=((15)/(2))/(4)`

`=(15)/(8)`

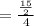
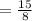
Therefore, the average rate of change from x = -1 to x = 3 will be:

Average rate = 15/8