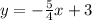Question

What is an equation of the line that passes through the point (8,-7)(8,−7) and is parallel to the line 5x+4y=165x+4y=16?

Answer 1

The equation of line parallel to given line passing through (8,-7) is:

`y = -(5)/(4)x+3`

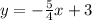
Explanation:

Given line is:

5x+4y=16

first of all, we have to convert the equation of given line in slope-intercept form

`4y = -5x+16`

Dividing both sides by 4

`(4y)/(4) = -(5x)/(4) + (16)/(4)\\y = -(5)/(4)x+4`

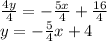
Slope intercept form is:

`y=mx+b`

The slope of given line is:

`m = -(5)/(4)`

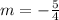
Let m1 be the slope of line parallel to given line

"The slopes of two parallel lines are equal"

`m = m_1\\m_1 = -(5)/(4)`

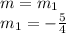
The equation of line parallel to given line will be:

`y = m_1x+b`

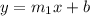
Putting the value of slope

`y = -(5)/(4)x+b`

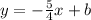
Putting the point (8,-7) in the equation

`-7 = -(5)/(4)(8)+b\\-7 = -(5)(2) + b\\-7 = -10+b\\b = -7 +10\\b = 3`

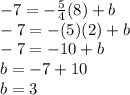
Putting the value of b

`y = -(5)/(4)x+3`

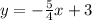
Hence,

The equation of line parallel to given line passing through (8,-7) is:

`y = -(5)/(4)x+3`