Question

Find the length and width of a rectangle whose area is 56 units squared and whose length is 10 units less than it's width

Answer 1

l = 4, w = 14

Explanation:

`A_r = 56 = l * w`

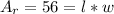
l - length;

w - width;

l = w - 10;

We substitute the 'l' using the previous formula =>

`[tex]A_r = (w -10) \cdot w = w^2 - 10w = 56 =>\\w^2 - 10w - 56 = 0\\`

By the quadratic formula we solve for 'w':(we will use the positive value, because we're talking about lengths of planes in a Euclidean space)

`w = (10 + √(100+224) )/(2) =  (10+18)/(2) = (28)/(2) = 14`

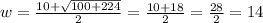
l = w - 10 = 14 -10 = 4