Question

What is the 19th term of a geometric sequence where a1=8 and a9=360. Round the common ratio and 19th term to the nearest hundredth.

REALLY need help on this one please please.

Answer 1

Explanation:

`a_(1) = 8\\a_(9) = 360 = a_(1) \cdot r^9 = 8 \cdot r^9\\r = \sqrt[9]{(360)/(9) }  \cong 1.53`

By the formula of a geometric series:

`S_(n) = a \cdot (1-r^n)/(1-r) => S_(19) = 8 \cdot (1-1.53^(19))/(1-1.53)  = 6091.54`

Answer 2

r = 1.6

a19 = 37800

Explanation:

First term
`a_1 = 8` and
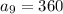`a_9 = 360` of a geometric sequence and we are to find the 19th term along with the common ratio for this sequence.

We know that the general term of a Geometric Sequence is given by:

`a_n= a \cdot r^(n-1)`

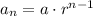
where
`a_n` is the nth term,
`a` is the first term,
`n` is the number of terms and
`r` is the common ratio.

Substituting the given values in the above formula to get:

`360 = (8)*(r)^(9-1)`

`360 = 8*(r^8)`

`r^8 = (360)/(8)`

`r^8 = 45`

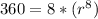
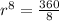
r = 1.6

Finding the 19th term:

`a_n= a \cdot r^(n-1)`

`a_(19)= 8 \cdot 1.6^(19-1)`

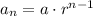
a19 = 37800