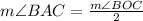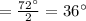Answer:
m∠BAC is 101° or 36°.
Explanation:
Given,
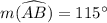
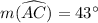
To find : The measurement of angle BAC,
Let O be the center of the circle.
Since, here we have to cases ( shown in diagram ),
In Case 1 :
![m\angle BOC = 360^(\circ)-[m(\widehat{AB})+m(\widehat{AC})]](https://img.qammunity.org/2020/formulas/mathematics/high-school/dq2guj2pmaaye9r3urbrrwimiei95iqtx9.png)
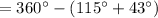
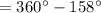
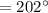
By the central angle theorem,
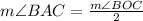
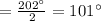
In Case 2 :
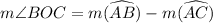
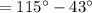
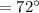
Again by the central angle theorem,