Final Answer:
The exact value of
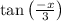 is
is
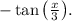
Step-by-step explanation:
To find the exact value of
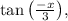 we can use the periodicity property of the tangent function. The tangent function has a period of
we can use the periodicity property of the tangent function. The tangent function has a period of
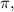 which means that
which means that
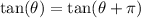 .
.
Therefore,
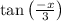 is equivalent to
is equivalent to
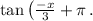 Additionally, the tangent function is an odd function, so
Additionally, the tangent function is an odd function, so
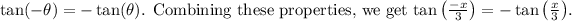
In summary, the exact value of
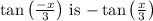 due to the periodicity and odd function properties of the tangent function.
due to the periodicity and odd function properties of the tangent function.