Question

PLEASE HELP! Points A and B split the circle into two arcs. Measure of minor arc is 150°. Point M splits major arc with the ratio 2:5 (point M is closer to point B). Find m∠BAM.

Answer 1

30 degrees

Explanation:

Answer 2

Answer: Measure of ∠BAM is 30°.

Step-by-step explanation:

As given in the question, points A and B split the circle with center O into two arcs in the attached figure below. Major of the minor arc is 150°. And, the point M splits the major arc in the ratio 2 : 5.

We are to find the measure of ∠BAM.

Since the measure of minor arc AB is 150°, so the measure of major arc AB will be

360° - 150° = 210°.

Also, point M divides the major arc AB in the ratio 2 : 5, so we have

`arc~BM:arc~MA=2:5.`

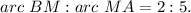
Therefore, the measure of ∠BOM is given by

`m\angle BOM=(2)/(2+5)*210^\circ=(2)/(7)* 210^\circ=60^\circ.`

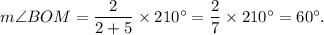
We know that

the measure of the angle subtended at the center by an arc is equal to twice the measure of the angle subtended at the circumference by the same arc.

That is, on arc BC, we get

`m\angle BOM=2* m\angleBAM\\\\\Rightarrow m\angle BAM=(m\angle BOM)/(2)\\\\\\\Rightarrow m\angle BAM=(60^\circ)/(2)\\\\\Rightarrow m\angle BAM=30^\circ.`

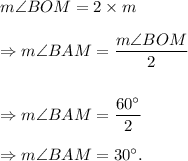
Thus, the measure of ∠BAM is 30°.