Question

Which of the following rules represents the function shown in the table?

Answer 1

This is F(n) = 3n

The X is an interger which is holding a value

The relationship between Y and X is 3n as we multiply X by 3 to get the value of Y and is proven yet so.

Answer 2

The rule which represent the function as shown in the table is:

`f(n)=3n`

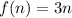
Explanation:

We are given a table as follows:

x 2 -1 0

y 6 -3 0

Now we are asked to find the function which represent these table of values.

a)

`f(n)=n+3`

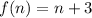
Here x is represented by n and y by f(n)

when n=2 we must have f(n)=6

Hence, we put n=2 in the given expression and check,

`f(2)=2+3=5\\eq 6`

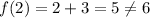
Hence, this is not a correct function.

b)

`f(n)=(1)/(3)n`

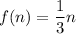
Again we check for n=2

We have:

`f(2)=(1)/(3)* 2=(2)/(3)\\eq 6`

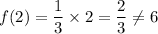
Hence, it is not a correct expression.

So we are left with option: c)

c)

`f(n)=3n`

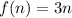
By putting the value of n=2,-1 and 0

we see that the expression matches the table of values.

( since,

when n=2 we have:

`f(2)=3* 2=6`

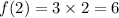
when n= -1 we have:

`f(-1)=3* -1=-3`

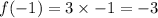
and when n=0 we have:

`f(0)=3* 0=0` )

Hence, this is a correct expression.