QUESTION 1
The given logarithm is
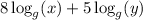
We apply the power rule of logarithms;
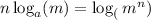

We now apply the product rule of logarithm;
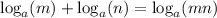
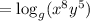
QUESTION 2
The given logarithm is
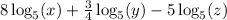
We apply the power rule of logarithm to get;
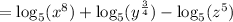
We apply the product to obtain;
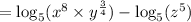
We apply the quotient rule;
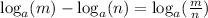
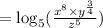
![=\log_5(\frac{x^8 \sqrt[4]{y^3} }{z^5})](https://img.qammunity.org/2020/formulas/mathematics/high-school/ngteevcbu278peihs2ct4us23iomq5re82.png)