a) The given function is
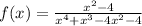
The domain refers to all values of x for which the function is defined.
The function is defined for
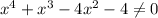
This implies that;
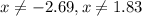
b) The vertical asymptotes are x-values that makes the function undefined.
To find the vertical asymptote, equate the denominator to zero and solve for x.
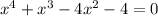
This implies that;
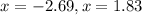
c) The roots are the x-intercepts of the graph.
To find the roots, we equate the function to zero and solve for x.

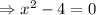
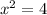
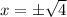

The roots are
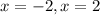
d) The y-intercept is where the graph touches the y-axis.
To find the y-inter, we substitute;
 into the function
into the function
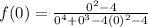
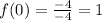
e) to find the horizontal asypmtote, we take limit to infinity

The horizontal asymtote is

f) The greatest common divisor of both the numerator and the denominator is 1.
There is no common factor of the numerator and the denominator which is at least a linear factor.
Therefore the function has no holes.
g) The given function is a proper rational function.
There is no oblique asymptote.
See attachment for graph.