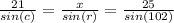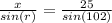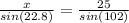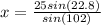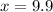Question

On a map, the North Carolina cities of Raleigh, Durham, and Chapel Hill form a triangle, as shown below. What are the approximate values of the missing measures on the map?

Answer 1

Answer: 1) r=23° , c=55° , x=10°

Explanation:

correct on edge 2020

Answer 2

The approximate values are:

c = 55.2°

r = 22.8°

x = 9.9 miles

Explanation

- To find angle
`c`, we are using the rule of sines:
`(a)/(sin(A)) =(b)/(sin(B)) =(c)/(sin(C))`

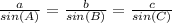
For our triangle
`a=21,A=c,b=x,B=r,c=25` and
`C=102`

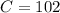
Replacing the values we get:
`(21)/(sin(c)) =(x)/(sin(r)) =(25)/(sin(102))`

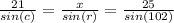
We can pick up two suited values to find
`c`:

`(21)/(sin(c)) =(25)/(sin(102))`

`21=(25sin(c))/(sin(102))`

`21sin(102)=25sin(c)`

`sin(c)=(21sin(102))/(25)`

`c=sin^(-1)((21sin(102))/(25))`

`c=55.2`

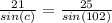
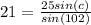
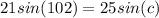
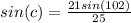
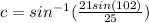
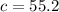
- Now that we have angle
`c`, we can use the angle sum theorem to find angle
`r`.

The angle sum theorem states the the interior angles of a triangle add up to 180°, so:

`r+c+102=180`

`r+55.2+102=180`

`r+157.2=180`

`r=22.8`

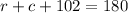
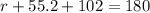
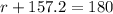
- Now that we have angle
`r`, we can use the rule of sines, one more time, to find side
`x`

`(21)/(sin(c)) =(x)/(sin(r)) =(25)/(sin(102))`

`(x)/(sin(r)) =(25)/(sin(102))`

`(x)/(sin(22.8)) =(25)/(sin(102))`

`x=(25sin(22.8))/(sin(102))`

`x=9.9`