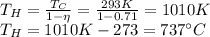Question

A carnot heat engine receives 600 kj of heat from a source of unknown temperature and rejects 175 kj of it to a sink at 20°c. determine (a) the temperature of the source and (b) the thermal efficiency of the heat engine.

Answer 1

(b) 71%

The thermal efficiency of a Carnot heat engine is given by:

`\eta = (W)/(Q_(in))`

where

W is the useful work done by the engine

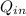`Q_(in)` is the heat in input to the machine

In this problem, we have:

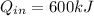`Q_(in)=600 kJ` is the heat absorbed

`W=600 kJ-175 kJ=425 kJ` is the work done (175 kJ is the heat released to the sink, therefore the work done is equal to the difference between the heat in input and the heat released)

So, the efficiency is

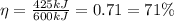
`\eta = (425 kJ)/(600 kJ)=0.71 = 71\%`

(a)
`737^(\circ)C`

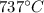
The efficiency of an engine can also be rewritten as

`\eta = 1-(T_C)/(T_H)`

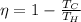
where

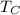`T_C` is the absolute temperature of the cold sink

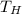`T_H` is the temperature of the source

In this problem, the temperature of the sink is

`T_C = 20^(\circ)C + 273=293 K`

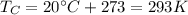
So we can re-arrange the equation to find the temperature of the source:

`T_H = (T_C)/(1-\eta)=(293 K)/(1-0.71)=1010 K\\T_H = 1010 K - 273=737^(\circ)C`