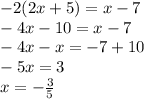Question

Solve the equation (linear equation)


`((16)/(9)) ^(2x +5) =((3)/(4))^(x-7)`

Answer 1

Answer:
`x=-(3)/(5)`

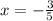
Explanation:

By the negative exponent rule, you have that:

`((1)/(a))^n=a^(-n)`

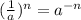
By the exponents properties, you know that:

`(m^n)^l=m^((nl))`

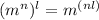
You can rewrite 16 and 9 as following:

16=4²

9=3²

Therefore, you can rewrite the left side of the equation has following:

`((4^2)/(3^2))^((2x+5))=((3)/(4))^((x-7))\\\\((3^2)/(4^2))^(-(2x+5))=((3)/(4))^((x-7))\\\\((3)/(4))^(-2(2x+5))=((3)/(4))^((x-7))`

As the base are equal, then:

`-2(2x+5)=x-7`

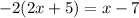
Solve for x:

`-2(2x+5)=x-7\\-4x-10=x-7\\-4x-x=-7+10\\-5x=3\\x=-(3)/(5)`