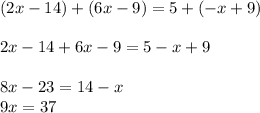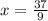Answer:
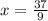
Explanation:
By the negative exponent rule, you have that:
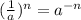
By the exponents properties, you know that:
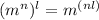
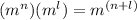
Rewrite 4, 8 and 32 as following:
4=2²
8=2³
32=2⁵
Rewrite the expression:

Keeping on mind the exponents properties, you have:
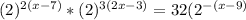
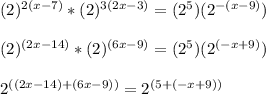
As the bases are equal, then: