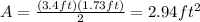Question

What is the area of this triangle?

Round to the nearest hundredth.

Answer 1

Answer: 2.94 ft²

Explanation:

Observe the figure attached:

The line LM divide the triangle into two right triangles.

Find the heigh "h" as following:

`sin\alpha=(opposite)/(hypotenuse)\\\\sin(40\°)=(h)/(2.7)\\\\h=(2.7)(sin(40\°))\\h=1.73ft`

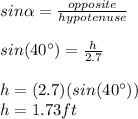
Apply the formula for calculte the area of a triangle:

`A=(Bh)/(2)`

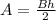
Where B (B=3.4 ft) is the base and h is the height (h=1.73ft)

Then:

`A=((3.4ft)(1.73ft))/(2)=2.94ft^2`