Question

Given: circle k (O) , m

PL
=80°,
m
PY
=150°
Find: m∠YPL

Answer 1

YL=130 (PWP)

m<YPL=65 (Inscribed < th)

Explanation:

Answer 2

`m\angle YPL=65^(\circ)`

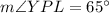
Explanation:

We have been given an image of a circle and we are asked to find the measure of angle YPL.

Since the degree measure of circumference of a circle is 360 degrees, so we can set an equation to find the measure of arc LY as:

`m\widehat{LY}+m\widehat{PL}+m\widehat{PY}=360^(\circ)`

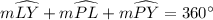
Upon substituting our given values in above equation we will get,

`m\widehat{LY}+80^(\circ)+150^(\circ)=360^(\circ)`

`m\widehat{LY}+230^(\circ)-230^(\circ)=360^(\circ)-230^(\circ)`

`m\widehat{LY}=130^(\circ)`

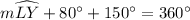
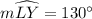
We can see that angle YPL is inscribed angle of arc LY, so the measure of angle YPL will be half the measure of arc LY.

`m\angle YPL=(1)/(2)m\widehat{LY}`

`m\angle YPL=(1)/(2)*130^(\circ)`

`m\angle YPL=65^(\circ)`

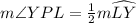
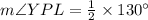
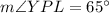
Therefore, the measure of angle YPL is 65 degrees.