Question

In what quadrant of the coordinate plane is the graph of the direct proportion located which is parallel to the graph, expressed by the formula:

Note: Please answer both questions in the same format (The direct proportion is ____. The graph is located on quadrants ___ and ___.).

Answer 1

Part 1) The direct proportion is
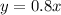`y=0.8x`. The graph is located on quadrants I and III

Part 2) The direct proportion is
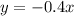`y=-0.4x`. The graph is located on quadrants II and IV

Explanation:

we know that

A relationship between two variables, x, and y, represent a proportional variation if it can be expressed in the form
`y=kx`

In a proportional relationship the constant of proportionality k is equal to the slope m of the line and the line passes through the origin

Part 1) we have

`y=0.8x-1.6`

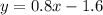
Remember that

If two lines are parallel, then their slopes are the same

In this problem, the slope of the given line is
`m=0.8`

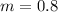
therefore

The direct proportion is
`y=0.8x`

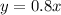
The graph is located on quadrants I and III

see the attached figure to better understand the problem

Part 2) we have

`y=-0.4+1`

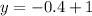
Remember that

If two lines are parallel, then their slopes are the same

In this problem, the slope of the given line is
`m=-0.4`

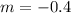
therefore

The direct proportion is
`y=-0.4x`

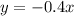
The graph is located on quadrants II and IV

see the attached figure to better understand the problem