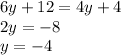Answer:
y = -4
Explanation:
Assuming the problem is
 , it would be nice if we could convert both sides of this equation to the same base; that way, we could compare the exponents directly in an equation of their own. Fortunately, 8 and 16 are both powers of 2 --
, it would be nice if we could convert both sides of this equation to the same base; that way, we could compare the exponents directly in an equation of their own. Fortunately, 8 and 16 are both powers of 2 --
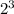 and
and
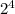 , we can rewrite the original equation by substituting those in:
, we can rewrite the original equation by substituting those in:
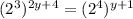
When you have an exponent raised to another exponent, you multiply those exponents together, so we can simplify our equation by distributing a 3 in the left exponent and a 4 in the right:
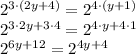
With both of our bases the same, we can now simply compare their exponents directly to solve for y: