Question

Jerome solved the equation below by graphing.

log2(x) + log2(x-2) = 3
Which of the following shows the correct system of equations and solution?

Answer 1

B. x = 4

Explanation:

I can't speak to the first part of this question, as I don't totally have context for what they're asking, but we can solve for x using one of the laws of logarithms, namely:

`\log_bm+\log_bn=\log_bmn`

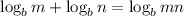
Using this law, we can combine and rewrite our initial equation as

`\log_2(x\cdot(x-2))=3\\\log_2(x^2-2x)=3`

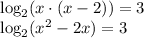
Remember that logarithms are simply another way of writing exponents. The logarithm
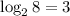`\log_28=3` is just another way of writing the fact
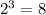`2^3=8`. Keeping that in mind, we can express our logarithm in terms of exponents as

`\log_2(x^2-2x)=3\rightarrow2^3=x^2-2x`

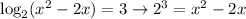
2³ = 8, so we can replace the left side of our equation with 8 to get

`8 = x^2-2x`

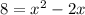
Moving the 8 to the other side:

`0=x^2-2x-8`

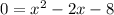
We can now factor the expression on the right to find solutions for x:

`0=(x-4)(x+2)\\x=4, -2`

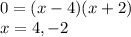
The only option which agrees with our solution is B.

Answer 2

The answer is:

`y_1=(\log x)/(\log 2)+(\log (x-2))/(\log 2)\ ,\ y_2=3\ ,\ x=4`

Explanation:

We are given a logarithmic expression as:

`\log_2 x+log_2 (x-2)=3`

As we know that:

`\log_a x=(\log x)/(\log a)`

Hence, we get the logarithmic expression as follows:

`(\log x)/(\log 2)+(\log (x-2))/(\log 2)=3`

We know that we can get the system of equations as follows:

`y_1=(\log x)/(\log 2)+(\log (x-2))/(\log 2)`

and

`y_2=3`

Hence, when we plot the graph for this system of equations we see that the point of intersection of the graph is: (4,3)

Hence, the solution is the x-value of the point of intersection of the two equations.

Hence, x=4 is the solution.

Hence, the correct option is:

`y_1=(\log x)/(\log 2)+(\log (x-2))/(\log 2)\ ,\ y_2=3\ ,\ x=4`