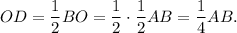Question

Prove: If a chord of a circle makes an angle of 30° with a diameter, prove that the distance from the center to the chord is one-fourth the length of the diameter.

Answer 1

See explanation.

Explanation:

Let BC be the diameter of the circle with center at point O, AB be the chord and ∠ABC=30°. OD is the distance from the center to the chord.

Consider triangle BDO. This triangle is special 30°-60°-90° right triangle. The leg OD is opposite to the angle of 30° and is half of the hypotenuse. The hypotenuse of the triangle BDO is BO. BO is the radius of the circle and is equal to half of the diameter AB. Thus,

`OD=(1)/(2)BO=(1)/(2)\cdot (1)/(2)AB=(1)/(4)AB.`