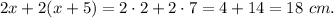Answer:
18 cm
Explanation:
Let the width of the rectangle be x cm, then the length of the rectangle is x+5 cm.
The area of the ractangle is
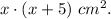
The area of the square with side's length of x cm is

The area of the square with side's length of x+5 cm is

The area of constructed figure is
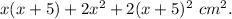
Since the total area of the constructed figure is 120 cm², you have
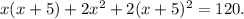
Solve this equation:

The width of the rectangle cannot be negative, so x=2 cm and x+5=7 cm and the perimeter of the rectangle is