Question

Use elimination to find the solution to the system of equations.

Answer 1

Hello!

The answer is:

B.

`x=-2\\y=-7`

Why?

Solving the system of equations by elimination, we have:

`\left \{ {{9x+3y=-39} \atop {4x+7y=-57}} \right.`

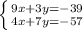
Then, multiplying the second equation by
`-(9)/(4)`

So,

`\left \{ {{9x+3y=-39} \atop {4x*(-(9)/(4)) +7y*(-(9)/(4)) =-57*(-(9)/(4))}} \right\\\\\left \{ {{9x+3y=-39} \atop {-9x-(63)/(4)y=(513)/(4) }} \right\\\\-(51)/(4)y=(357)/(4)\\\\y=(357)/(4)*(-(4)/(51))=-(1428)/(204)=-7`

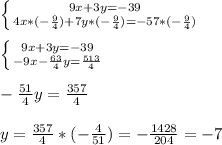
Then, substituting y=-7 into the first equation (also, we could substitute it into the first equation) we have:

`9x+3(-7)=-39\\9x-21=-39\\9x=-39+21\\9x=-18\\x=(-18)/(9)=-2`

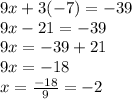
So, the solutions for the system of equations are:

`x=-2\\y=-7`

Have a nice day!

Answer 2

Answer: option B.

Explanation:

You can apply the elimination method:

- Multiply the first equation by -7 and the second equation by 3.

- Add both equations to cancel out the variable y.

- Solve for x

`\left \{ {{(-7)9x+3y=(-39)(-7)} \atop {(3)(4x+7y)=(-57)(3)}} \right.\\\\\left \{ {{-63x-21y=273} \atop {12x+21y=-171}} \right.\\-------\\-51x=102\\x=-2`

- Substitute x=-2 into any of the original equations ans solve for y. Then:

`9(-2)+3y=-39\\-18+3y=-39\\3y=-21\\y=-7`