Question

Retro Rides is a club for owners of vintage cars and motorcycles. Every year the club gets together for a ride. This year, 38 vehicles participated in the ride. The total number of tires of all the vehicles was 104. Assuming each car has 4 tires and each motorcycle has 2 tires, how many each of cars and motorcycles participated in the ride?

A. 18 cars; 20 motorcycles
B. 14 cars; 24 motorcycles
C. 11 cars; 27 motorcycles
D. 16 cars; 22 motorcycles

Answer 1

Hello!

The answer is:

Option B.

`Cars=14\\Motorcycles=24`

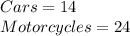
Why?

We know that the total of tires of all the vehicles was 104, and there were 38 vehicles with 4 tires and motorcyles with 2 tires, so, we can calculate how many cars and motorcyles participated in the ride using the following equation:

Let x be the cars and y be the motorcyles, so:

`x+y=38`

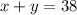
and,

`4x+2y=104`

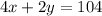
So, isolating x in terms of y from the first equation, we have:

`x=38-y`

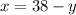
Then, substituting "x" into the second equation we have:

`4(38-y)+2y=104\\152-4y+2y=104\\152-2y=104\\2y=152-104\\2y=48\\y=(48)/(2)=24`

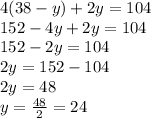
Now, substituting "y" into the first equation, we have:

`x+24=38`

`x=38-24=14`

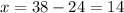
So, there were a total of 14 cars and 24 motorcycles in the ride.

Have a nice day!

Answer 2

Answer: OPTION B

Explanation:

Let's call:

c: the number of cars.

m: the number of motorcycles.

Based on the given information, you can set up the following system of equations:

`\left \{ {{c+m=38} \atop {4c+2m=104}} \right.`

You can solve it by the Elimination method:

- Multiply the first equation by -4.

- Add both equations to cancel out the variable "c".

- Solve for "m":

`\left \{ {(-4)(c+m)=38(-4)} \atop {4c+2m=104}} \right.\\\\\left \{ {-4c-4m=-152} \atop {4c+2m=104}} \right.\\-------\\-2m=-48\\m=24`

(24 motorcycles)

- Substitute m=24 into any of the original equations ans solve for "c". Then:

`c+24=38\\c=38-24\\c=14`

(14 cars)