1 Answer

Ortund · Answer 1 · 2020-08-01T16:39:47+0000

1. The given curves intersect one another three times:

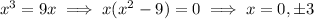
$x^3=9x\implies x(x^2-9)=0\implies x=0,\pm3$

The area of the bounded region is

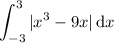
$\displaystyle\int_(-3)^3|x^3-9x|\,\mathrm dx$

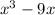x^3-9x is odd, but the absolute value makes it even. More formally,

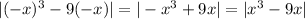
|(-x)^3-9(-x)|=|-x^3+9x|=|x^3-9x|

which means the integral is equivalent to

$\displaystyle2\int_0^3|x^3-9x|\,\mathrm dx$

For
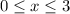$0\le x\le 3$ , the definition of absolute value tells us that

|x^3-9x|=9x-x^3

so the integral evaluates to

$\displaystyle2\int_0^3(9x-x^3)\,\mathrm dx=\left(9x^2-\frac{x^4}2\right)\bigg|_(x=0)^(x=3)=\frac{81}2=40.5$

2. Using the disk method, the volume is given by the integral

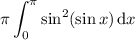
$\displaystyle\pi\int_0^\pi\sin^2(\sin x)\,\mathrm dx$

Use a calculator to get the result 1.219.

Please log in or register to add a comment.