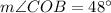1 Answer

Alexander Jank · Answer 1 · 2020-12-16T14:27:02+0000

The alternate segment theorem says that angles BAC and BCE are congruent, so

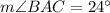
$m\angle BAC=24^\circ$

###

Triangle ABC is isosceles, which makes angles ACB and ABC congruent, and the sum of the interior angles of any triangle is 180 degrees, so

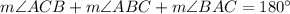
$m\angle ACB+m\angle ABC+m\angle BAC=180^\circ$

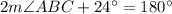
$2m\angle ABC+24^\circ=180^\circ$

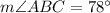
$m\angle ABC=78^\circ$

###

The alternate segment theorem also says that angles DCF and CAD are congruent. Angles DCF, ACD, ACB, and BCE are supplementary, so

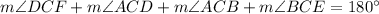
$m\angle DCF+m\angle ACD+m\angle ACB+m\angle BCE=180^\circ$

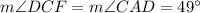
$m\angle DCF=m\angle CAD=49^\circ$

Then

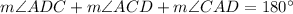
$m\angle ADC+m\angle ACD+m\angle CAD=180^\circ$

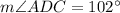
$m\angle ADC=102^\circ$

###

The inscribed angle theorem says that angle COB has twice the measure of angle BAC, so

$m\angle COB=48^\circ$

Please log in or register to add a comment.