Answer:
0.7325 to 5.6675 ug/dl
Explanation:
The middle 90% will be 45% above the mean and 45% below the mean. This means
0.5-0.45 = 0.05 and
0.5+0.45 = 0.95
We use a z table. Look in the cells; find the values as close to 0.05 and 0.95 as we can get.
For 0.05, we have 0.0505 and 0.0495; since these are equidistant from 0.05, we use the value between them. 0.0505 is z=-1.64 and 0.0495 is z=1.65; this gives us z=-1.645.
For 0.95, we have 0.9495 and 0.9505; since these are equidistant from 0.95, we use the value between them. 0.9495 is z = 1.64 and 0.9505 is z=1.65; this gives us z = 1.645.
Now we use our z score formula,
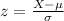
Our two z scores are 1.645 and -1.645; our mean, μ, is 3.2; and our standard deviation, σ, is 1.5:
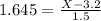
Multiply both sides by 1.5:
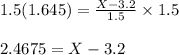
Add 3.2 to each side:
2.4675+3.2 = X-3.2+3.2
5.6675 = X
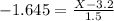
Multiply both sides by 1.5:

Add 3.2 to each side:
-2.4675+3.2 = X-3.2+3.2
0.7325 = X
Our range is from 0.7325 to 5.6675.