Answer:
27 times
Explanation:
Given that sphere A is similar to sphere B
Let radius of sphere B be x. Then the radius of
sphere A be 3 times radius of sphere B = 3x
Volume of sphere A =
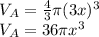
Volume of sphere B =

Ratio would be
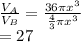
i.e. volume of sphere is 27 times volume of sphere B.