Question

Which Of the following could not be points on the units circle ?

Answer 1

answer A , that could not be point

Answer 2

Options a and c

Explanation:

A unit circle is one which has origin as centre and radius as 1.

The equation of the unit circle would be

`x^2+y^2 =1`

Thus we find that any point satisfying the above equation lies on the unit circle

Let us try the given points one by one

a)
`(0.8)^2+(-0,6)^2 =1`. Hence lies on the circle

b) (1,1)

Cannot lie on circle since
`1^2+1^2 \\eq 1`

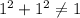
c)
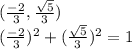`((-2)/(3) ,(√(5) )/(3) )\\((-2)/(3))^2+((√(5) )/(3) )^2 =1`. Hence lies on the circle

d)
`((√(3) )/(2) ,(1)/(3) )\\((√(3) )/(2))^2+((1)/(3) )^2\\\\eq 1`

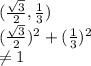
Hence does not lie on the circle

Only option A,C are right