Question

Jason and Shawn both begin riding their bikes from different points away from the ranger station. They both ride their bikes in the direction away from the station along the same trail.

Jason starts biking 1 mile away from the station. Jason rides at a constant speed of 20 miles per hour.

Shawn starts biking 2 miles away from the station. Shawn rides at the same constant speed as Jason.

Let y represent the total miles away from the station.

At how many hours, x, will it take Shawn to catch up with Jason?

Based on the information provided, complete each expression below and determine the number of solutions.

Answer 1

Hello!

The answer is: There is no solution, it's not possible for Shawn to catch up with Jason since both are riding at the same constant speed, there is always be a distance of 1 mile between.

Why?

If it's possible to Shawn to catch up with Jason, the following equation will be true:

Let be the station our origin, so:

`ShawnPosition=JasonPosition\\20mph.x-2miles=20mph.x-1mile\\-2=-1`

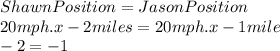
So, since the equation is not fulfilled, there is not solution, meaning that it's not possible to Shawn to catch up with Jason since both started riding from different points keeping the same constant speed, there will always be a distance of 1 mile between them if they keep the speed constant.

Also, Shawn could have caught up with Jason if he were started with a speed of 21mph instead the Jason speeds (20mph), let's prove that:

`ShawnPosition=JasonPosition\\21mph.x-2miles=20mph.x-1mile\\\\21mph.x-20mph.x=2miles-1mile\\\\mph.x=1mile\\x=1h`

So, by substituting "x" into the equations, we have:

`ShawnPosition=JasonPosition\\21mph.1h-2mile=20mph.1h-1mile\\21miles-2miles=20miles-1mile\\19miles=19miles`

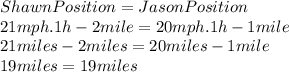
So, Shawn could have caught up with Jason if he were started with a 21 mph speed instead starting with the Jason speed (20 mph).

Have a nice day!