Choose an equation that when paired with the equation below, will create a system of equations with infinitely many solutions, one solution, or no solutions.

Question

asked Oct 18, 2020 89.7k views

1 Answer

Darryl Wilson · Answer 1 · 2020-10-25T02:38:11+0000

Answer:

Infinitely many solutions:

One solution:

No solution:

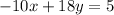
Explanation:

Solve for y from each equation to obtain the equation of the line in slope-intercept form:

y=mx+b

m: slope

b: y-intercept

EQUATION ON THE TOP:

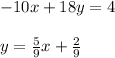
$-10x+18y=4\\\\y=(5)/(9)x+(2)/(9)$

Equation 1:

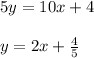
$5y=10x+4\\\\y=2x+(4)/(5)$

The equation on top and the equation equation 1 has different slopes and different y-intercept, therefore the system will have one solution.

Equation 2:

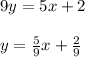
$9y=5x+2\\\\y=(5)/(9)x+(2)/(9)$

The equation on top and the equation equation 2 are the same, therefore, the system will have infinitely many solutions.

Equation 3:

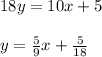
$18y=10x+5\\\\y=(5)/(9)x+(5)/(18)$

The slopes are equal, then both lines will be parallels, therefpre the system will have no solution.