Question

(a) A box with its contents has a total mass of 20 kg. It is dropped from a very high building. After reaching terminal speed, what is the magnitude of the air resistance force acting upward on the falling box? N (b) The box survived the fall and is returned to the top of the building. More objects are put into the box, and the box with its contents now has a total mass of 65 kg. The box is dropped, and it reaches a higher terminal speed than before. After reaching terminal speed, what is the magnitude of the air resistance force acting upward on the falling box? (The fact that the heavier object reaches a higher terminal speed shows that the air resistance force increases with increasing speed.)

Answer 1

(a) 196 N

At terminal speed, the velocity of the box is constant: this means that its acceleration is zero, so according to Newton's second Law, the resultant of the forces acting on the box is zero. Since there are only two forces acting on the box:

- The weight, acting downward:
`W = mg`

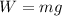
- The air resistance, acting upward:
`R`

It means that at terminal speed, the two forces are balanced:

`W-R=0`

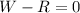
So we have:

`R=W=mg=(20 kg)(9.8 m/s^2)=196 N`

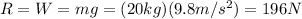
(b) 637 N

The exercise is exactly identical as before, but this time the mass of the box is different: m = 65 kg. Therefore, the air resistance in this case will be:

`R=W=mg=(65 kg)(9.8 m/s^2)=637 N`