Explanation:
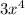 x +
x +
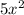 x + x - 1
x + x - 1
—————————--------------
x
Simplify
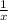
(((3 • (x3)) + 5x) -
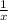 ) + 1
) + 1
3.1 Subtracting a fraction from a whole
Rewrite the whole as a fraction using x as the denominator :
3x^3 + 5x (3x^3 + 5x) • x
3x^3 + 5x = ———————— = ——————————————
1 x
Equivalent fraction : The fraction thus generated looks different but has the same value as the whole
Common denominator : The equivalent fraction and the other fraction involved in the calculation share the same denominator
4.1 Pull out like factors :
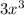 + 5x
+ 5x
![(3x^3 + 5x)/(1) = \frac{(3x^3 + 5x) [tex]3x^(3) + 5x = x • (3x^2 + 5)]() x}{x}[/tex]
x}{x}[/tex]
5.1 Adding a whole to a fraction
Rewrite the whole as a fraction using x as the denominator :
1 1 • x
1 = — = —————
1 x