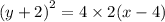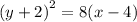ANSWER
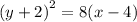
EXPLANATION
The given parabola has equation of the form

where (h,k) is the vertex of the parabola.
The vertex of the given parabola is (4,-2).
and p is the distance between the foci and the vertex.
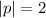
The parabola opens towards the positive x-axis, therefore p=2.
Hence the equation of the parabola is