Question

Justin Bieber is thrown horizontally at 10.0m/s from the top of a cliff 122.5 m high.

How long does it take to reach the ground?
What is the horizontal displacement?
What is Justin's final velocity?

Answer 1

Explanation:

How long it takes to reach the ground is a y-dimension thing, and horizontal displacement is an x-dimension thing. So let's set up a table with the info we have in each dimension:

x y

V₀ 10.0 m/s 10.0 m/s

Δx ? -122.5 m

a 0 m/s/s -9.8 m/s/s

v 10.0 m/s ?

t ? ?

That seems like an awful lot of question marks, doesn't it?

The first question asks us for the time, t, it takes for the pathetic and greatly disliked Justin Bieber to hit the ground. We will use the equation:

Δx = V₀t + 1/2at²

Filling in our values using the y-dimension stuff only:

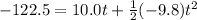`-122.5 = 10.0t+(1)/(2)(-9.8)t^2` which simplifies to

`-122.5=10.0t-4.9t^2`

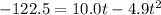
Hmmm...this is beginning to resemble a parabolic equation you probably already studied in Algebra 2!

We can solve for t by getting everything on one side and setting the equation equal to 0. We set it equal to 0 since the height on the ground is 0:

`-4.9t^2+10.0t+122.5=0`

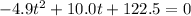
When you factor that for the 2 values of t, you get

t = -4.1 and 6.1

Of course, since time can't EVER be negative, we use a t value of 6.1. That's how long it takes to hit the ground. That t value can now be filled into the t values in our table above. We need that t value for the next part that asks us the horizontal displacement, Δx. This is x-dimension stuff now. Using the same equation:

Δx =
`10.0(6.1)+(1)/(2)(0)(6.1)^2`

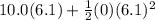
Of course since the acceleration in the x-dimension is always 0, the whole portion of the equation after the equals sign is eliminated, leaving us with

Δx = 10.0(6.1)

Δx = 61 m

Poor Justin, upon his demise, hits the ground. Therefore, his final velocity is 0, since his body met the ground and stopped dead.