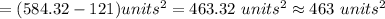The diagram below shows a square inside a regular octagon. The apothem of the octagon is 13.28 units. To the nearest square unit, what is the area of the shaded region?

Question

asked Jun 21, 2020 123k views

2 Answers

Volker · Answer 1 · 2020-06-24T19:35:22+0000

Answer:

The correct option is: A. 463 square units.

Explanation:

According to the given diagram, the side length of the regular octagon is 11 units.

So, the perimeter
(p) of the octagon
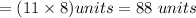
$=(11* 8)units= 88\ units$

The apothem
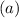(a) of the octagon is 13.28 units.

So, the area of the octagon:
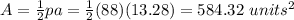
$A=(1)/(2)pa=(1)/(2)(88)(13.28)=584.32\ units^2$

Now, the side length of the inside square is 11 units. So, the area of the square
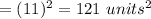
$=(11)^2 =121\ units^2$

Thus, the area of the shaded region
$=(584.32-121)units^2=463.32\ units^2 \approx 463\ units^2$