Answer:
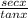 = cscx
= cscx
Explanation:
We have given a trigonometric expression.
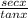
We have to simplify the above expression.
Since, we know that
secx is reciprocal of cosx.
secx = 1/cosx
Tanx is the ratio of sinx and cosx.
Tanx = sinx / cosx
Given expression becomes
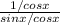
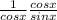
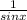
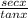 = cscx which is the answer.
= cscx which is the answer.