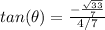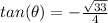Question

Find sin and tan (Picture provided)

Answer 1

Option C.
`sin(\theta)=-(√(33))/(7)` ,
`tan(\theta)=-(√(33))/(4)`

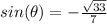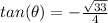
Explanation:

we know that

If cosine of angle theta is positive then angle theta belong to the I or IV quadrant

and

If co secant of angle theta is negative then angle theta belong to the III or IV quadrant

therefore

angle theta belong to the IV quadrant (common solution)

Part 1) Find
`sin(\theta)`

we know that

`sin^(2) (\theta)+cos^(2) (\theta)=1`

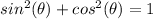
we have

`cos(\theta)=4/7`

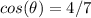
substitute the value

`sin^(2)(\theta)=1-(4/7)^(2)`

`sin^(2)(\theta)=1-(16/49)`

`sin^(2)(\theta)=(33/49)`

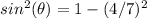
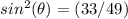
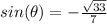`sin(\theta)=-(√(33))/(7)` ----> is negative because the angle belong to the IV quadrant

Part 2) Find
`tan(\theta)`

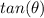
we know that

`tan(\theta)=(sin(\theta))/(cos(\theta))`

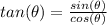
we have

`sin(\theta)=-(√(33))/(7)`

`cos(\theta)=4/7`

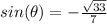
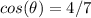
substitute the values

`tan(\theta)=(-(√(33))/(7))/(4/7)`

`tan(\theta)=-(√(33))/(4)`