Answer: See below
Step-by-step explanation:
Given:
The potential between plates, V = 240 V
Distance between plates, d = 0.02 m
The mass of drop, m = 2x10^-11
Charge on electron, e = 1.6x10^-19
Part (a)
The free-body diagram is attached below
Part (b)
The electric field is given by,
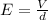
On applying force balance, the force on oil drop is equal to the weight of the oil,
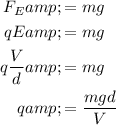
Substituting the given values in the above equation,
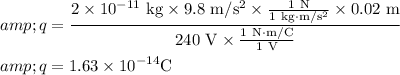
Therefore, the charge on the oil drop is 1.63x10^-14 C
Part (c)
There will be an excess of electrons on the oil drop.
The number of electrons on oil drop can be calculated as,
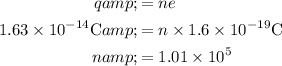
Therefore, the number of excess electrons is 1.01x10^5