Question

Simplify the expression (Picture provided)

Answer 1

b. secx

Explanation:

We have given a trigonometric expression.

csc(x)/cot(x)

We have to simplify it.

Since we know that

csc(x) is reciprocal to sin(x).

cscx = 1/sinx

cot(x) is ratio of cos(x) and sin(x).

cotx = cosx/sinx

Then, given expression becomes,

`(1/sinx)/(cosx/sinx)`

`(1)/(sinx)` ×
`(sinx)/(cosx)`

`(1)/(cosx)`

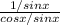
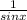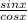
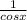
csc(x)/cot(x) = secx

Answer 2

Answer:


`\sec(\theta)`

Explanation:

We want to simplify


`(\csc(\theta))/(\cot(\theta))`

We express in terms of the sine and cosine ratios to obtain;


`((1)/(\sin(\theta)) )/((\cos(\theta))/(\sin(\theta)) )`

This is the same as


`(1)/(\sin(\theta)) / (\cos(\theta))/(\sin(\theta))`

Multiply by the reciprocal to get;


`(1)/(\sin(\theta)) * (\sin(\theta))/(\cos(\theta))`

Cancel the common factors;


`(1)/(\cos(\theta))=\sec(\theta)`