Answer:
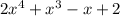
Explanation:
To find which one is prime, let's try to factor them all. We can use the factoring by grouping method.
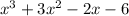
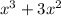 and
and
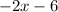
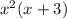 and
and
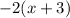
So this one is not prime, since you can still factor it.
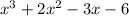
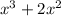 and
and
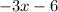
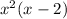 and
and
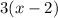
So this one is not prime, since you can still factor it.
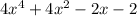
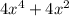 and
and
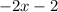
 and
and
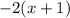
So this one is not prime, since you can still factor it.
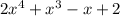
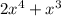 and
and
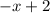
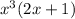 and -x+2 cannot be further factored.
and -x+2 cannot be further factored.
Therefore,
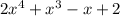 is a prime.
is a prime.