Answer:
32 square units
Explanation:
A rectangle has vertices at (-1, 6), (-1, -2), (3, 6), and (3,-2)
Area of a rectangle = length times width
LEts find the distance between (-1, 6) and (3, 6)
Apply distance formula


LEts find the distance between (-1, 6), (-1, -2)
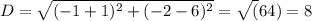
Area of the rectangle = 4 times 8= 32 square units