Question

What is a formula for the nth term of a given sequence

-12,-16,-20...
an = -12(-4)^n
a^n = -12 - 4 (n+1)
an = -8 - 4n
an = -12(-4)^n-1

Answer 1

`a_(n) = -12-4(n-1)`

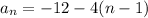
Explanation:

We have given a arithmetic sequence.

-12,-16,-20,...

We have to find formula for a given sequence.

The general formula for nth term of sequence is :

`a_(n) = a_(1)+d(n-1)`

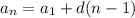
In given sequence,

`a_(1) = -12`

d is the common difference between consecutive terms.

d = -16-(-12) = -16+12

d = -4

Putting given values in formula, we have

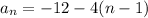`a_(n) = -12-4(n-1)` which is the answer.

Answer 2

`a_n=-12-4(n-1)`

Explanation:

The given sequence is

-12,-16,-20...

The first term of this sequence is
`a_1=-12`.

The common difference is

`d=-16--12`

`d=-16+12=-4`

The nth term of this arithmetic sequence is;

`a_n=a_1+d(n-1)`

We substitute the values for the first term and the common difference to obtain;

`a_n=-12-4(n-1)`