Answer:
The correct answer option is C. a=3, b=4.
Explanation:
We are given the following expression and we need to determine whether which of the values of
 and
and
 should be used to make the equation true:
should be used to make the equation true:
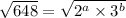
A. a=3, b=2:
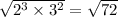
B. a=2, b=3:

C. a=3, b=4 :
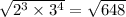
D. a=4, b=3:
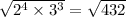
Therefore, the correct answer option is C. a=3, b=4.