Question

Two cyclists, Alan and Brian, are racing around oval track of length 450m on the same direction simultaneously from the same point. Alan races around the track in 45 seconds before Brian does and overtakes him every 9 minutes. What are their rates, in meters per minute?

Answer 1

Alan: 200 m/min

Brian: 150 m/min

Step-by-step explanation:

Given : Two cyclists, Alan and Brian, are racing around oval track of length 450m on the same direction simultaneously from the same point. Alan races around the track in 45 seconds before Brian does and overtakes him every 9 minutes.

To find : What are their rates, in meters per minute?

Solution :

Let n represent the number of laps that Alan completes in 9 minutes.

Then n-1 is the number of laps Brian completes.

45 seconds = 3/4 minutes.

The difference in their lap times in minutes per lap is

`(9)/((n -1))-(9)/(n) =(3)/(4)`

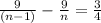
Solving the equation we get,

`(9n-9n+9)/(n(n -1)) =(3)/(4)`

`9* 4=3* n(n -1)`

`36=3* n(n -1)`

`n^2-n-12=0`

`n^2-4n+3n-12=0`

`n(n-4)+3(n-4)=0`

`(n-4)(n+3)=0`

`n=4,-3`

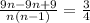
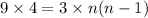
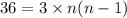
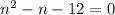
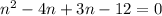
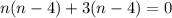
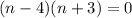
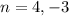
Neglecting n=-3

So, n=4

Then Alan's speed in m/min is

`S=(D)/(T)`

`S_a=(4* 450)/(9)`

`S_a=200 m/min`

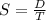
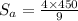
Brian completes 3 laps in that 9-minute time, so his rate is

`S_b=(3* 450)/(9)`

`S_b=150 m/min`

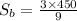
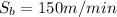
Therefore, Alan: 200 m/min

Brian: 150 m/min