Answer:
Hence, the area of the rectangular space is:
284.6667 square yards.
Explanation:
It is given that the length(l) of the rectangular space is:
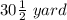 .
.
which in improper fraction is:
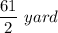
Similarly, the width(b) of the rectangular space is:
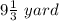
which in improper fraction is:
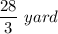
As we know that the area of the rectangular space is calculated as:
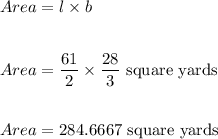
Hence, Area is: 284.6667 square yards.