Question

What is the sum of the geometric series ?

Answer 1

Answer: The required sum is 259.

Step-by-step explanation: We are given to find the sum of the following geometric series :

`\sum_(i=1)^(4)6^(i-1).`

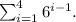
The given geometric series can be written as :

`0+6+6^2+6^3.`

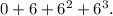
We know that

the sum of a geometric series up to n terms with first term a and common ration r is given by

`S=(a(r^n-1))/(r-1).`

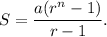
in the given series, we have

`a=1,~~r=(6)/(1)=(6^2)/(6)=(6^3)/(6^2)=6.`

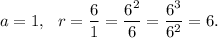
Therefore, the sum up to 4 terms will be

`S_4=(a(r^4-1))/(r-1)=(1(6^4-1))/(6-1)=(1296-1)/(5)=(1295)/(5)=259.`

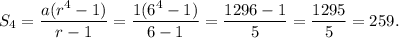
Thus, the required sum is 259.

Answer 2

Replace t with 1 through 4 and solve then add them together:

6^(1-1) = 6^0 = 1

6^(2-1) = 6^1 = 6

6^(3-1) = 6^2 = 36

6^(4-1) = 6^3 = 216

Sum = 1 + 6 + 36 +216 = 259