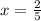Answer:
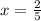 or
or

Explanation:
The given quadratic equation is

Group the constant terms on the right hand side.
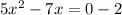
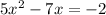
Divide through by 5.
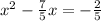
Add the square of half the coefficient of x., which is
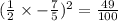 to both sides of the equation.
to both sides of the equation.
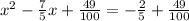
The left hand side is now a perfect square.
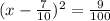
Take the square root of both sides;
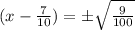
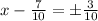
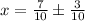
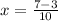 or
or
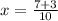
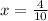 or
or
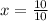
 or
or