Question

Estimate the limit.

Answer 1

The correct answer option is A. 0.25.

Explanation:

We are given the following expression and we are to find its limit:

`lim_\left \{ {{ x = 2 }`
`\frac { x - 2 } { x ^ 2 - 4 }`.

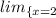
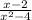First of all, we will simplify the expression by factorizing the term in the denominator:

`\frac { x - 2 } { x ^ 2 - 4 } = \frac { x - 2 } { ( x - 2 ) ( x + 2 ) }`

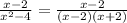
Cancelling the common terms to get:

`(1)/(x+2)`

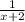
Substituting the given value for x to get:

`(1)/(2+2)` = 0.25

Answer 2

a. 0.25

Explanation:

The given expression is

`\lim_(x \to 2) (x-2)/(x^2-4)`

Factor the denominator using difference of two squares.

`\lim_(x \to 2) (x-2)/((x-2)(x+2))`

Cancel out common factors;

`\lim_(x \to 2) (1)/((x+2))`

We plug in 2 to get

`\lim_(x \to 2) (1)/((x+2))=(1)/(2+2)`

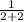`\lim_(x \to 2) (1)/((x+2))=(1)/(4)=0.25`