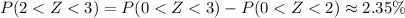900 = 750 + 2*75. In other words, 900 is 2 standard deviations away from the mean. Similarly, 975 is 3 standard deviations from the mean. So
![P(900<X<975)=P(2<Z<3)[/tex</p><p>where [tex]X](https://img.qammunity.org/2020/formulas/mathematics/middle-school/ukfoa3kaz46ftxyhx8s1r0wvvk6mk9x4ir.png) is the random variable for the lifespan of a light bulb with the given normal distribution, and
is the random variable for the lifespan of a light bulb with the given normal distribution, and
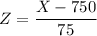 with the standard normal distribution.
with the standard normal distribution.
We get
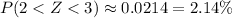
If you don't have a calculator/lookup table available, you can invoke the empirical rule, the one that says
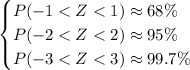
The normal distribution is symmetric about its mean, so we also know
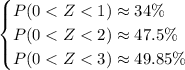
Then