Question

Graph the solution for the following system of inequalities. Click on the graph until the correct solution is displayed. x + y > 3 x + y < -4

Answer 1

This is the correct graph on Odyssey :)

Answer 2

The graph for the following system of inequalities is attached below.

Explanation:

The given system of inequalities is

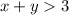`x+y>3` .... (1)

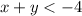`x+y<-4` .... (2)

From inequality (1) and (2) it is clear that (x+y) is greater than 3 adn 3 is not less than -4. So, the given system of inequality has no feasible reason or solution.

The related equation of first inequality is

`x+y=3`

Put x=0 to find the y-intercept.

`0+y=3\Rightarrow y=3`

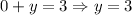
The y-intercept is 3.

Put y=0 to find the x-intercept.

`x+0=3\Rightarrow x=3`

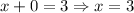
The x-intercept is 3.

The related equation of second inequality is

`x+y=-4`

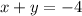
Put x=0 to find the y-intercept.

`0+y=-4\Rightarrow y=-4`

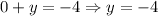
The y-intercept is -4.

Put y=0 to find the x-intercept.

`x+0=-4\Rightarrow x=-4`

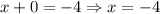
The x-intercept is -4.

The related lines are dotted line because the sign of inequalities are > and <.

Check each inequality be (0,0).

`0+0>3`

`0>3`

This statement is false. So the shaded region of first inequality is opposite sides of the origin.

`0+0<-4`

`0<-4`

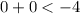
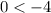
This statement is false. So the shaded region of first inequality is opposite sides of the origin.

The graph for the following system of inequalities is attached below.